Physics task rear window?
Greetings, a physics problem has me thinking a bit.
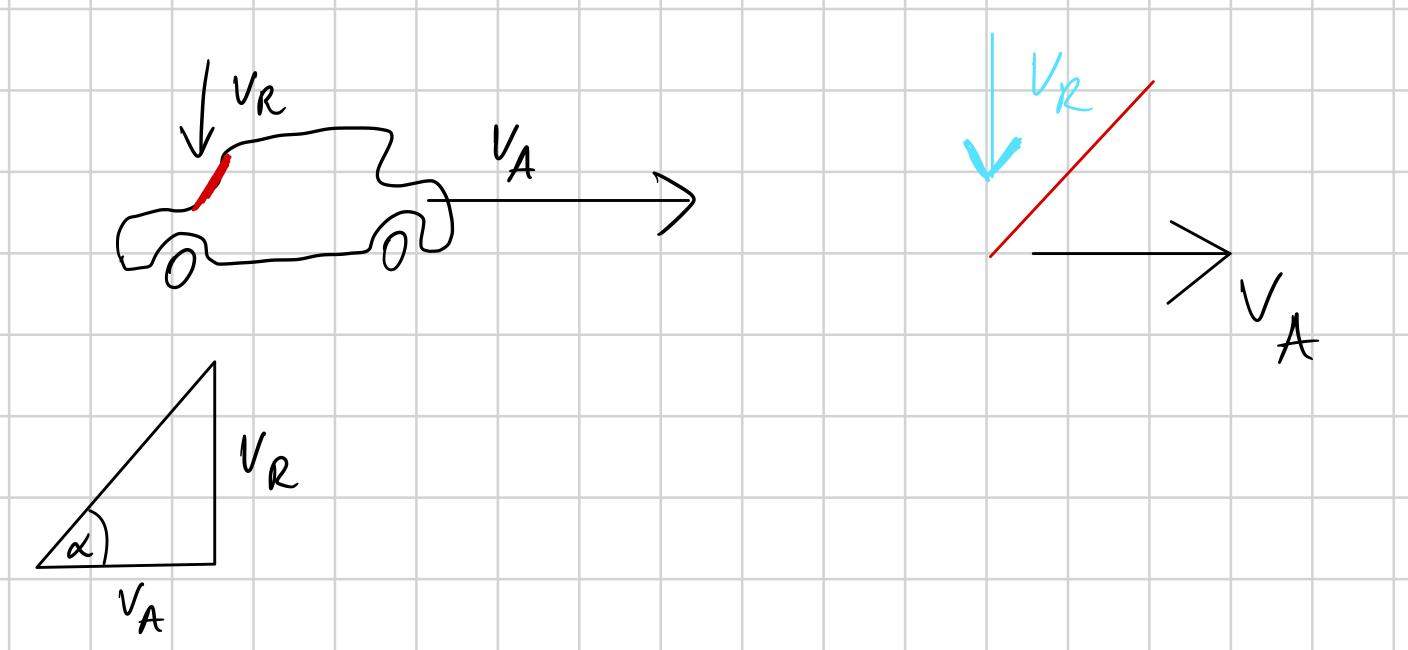
It's about how fast the car has to go to prevent the rear window from getting wet. Values aren't necessary, as I need help understanding them. The rain is falling vertically from above, the rear window is red, and the car's speed is represented by a black arrow.
To solve the problem, the arrows were moved so that they formed a right-angled triangle with the rear window. Then, using alpha, the tangent was calculated.
1) In such tasks, can I always move the “arrows” as I want?
2) How do I know where to set alpha? In this example, there's a right angle, so there are only two corners where you can set alpha. But otherwise, you could set alpha at three corners.
Es kann helfen, die Situation im Bezugssystem des Fahrzeugs zu betrachten, d.h. in einem Bezugssystem, das sich mit der Geschwindigkeit v_A relativ zur Strasse bewegt und in dem das Auto ruht.
Nun betrachtet man die Bahn eines Regentropfens in diesem Bezugssystem: der Regentropfen hat neben der vertikalen Komponente Geschwindigkeitskomponente v_R eine Geschwindigkeitskomponente v_A nach links, entgegen der Fahrtrichtung des Fahrzeugs. Die Scheibe wird genau dann nicht nass, wenn die Bahn des Regentropfens parallel zur Heckscheibe verläuft.
Ich glaube das kannst Du so nicht rechnen, da die Luftbewegung und somit die Bewegung der Regentropfen, nicht berücksichtigt wird.
Nach Deiner Theorie müsste das Auto nur schneller fahren als die Regentropfen fallen bei 45 Grad. In der Praxis wird aber trotzdem alles nass werden.
Die Lösung, von der ich spreche, wurde von dem Prof während der Physik Vorlesung besprochen. Ich hatte seit einer Ewigkeit kein Physik, weshalb mir hier das Verständnis fehlt
Der Einwand des Elektroheizers stimmt. Aber wahrscheinlich dient dieses Beispiel mit dem Auto ja nur dazu, Euch das Denken mit Vektoren nahezubringen. Beispiele für den Unterricht sind immer vereinfacht. Oft sind sie so sehr vereinfacht, dass sie mit der Wirklichkeit nur wenig übereinstimmen. Geh einfach davon aus, dass Du hier eigentlich nichts über Autos im Regen lernen sollst, sondern ein paar Grundlagen davon, wie man mit Vektoren über bewegte Körper und Geschwindigkeiten nachdenkt. Wer damit umzugehen gelernt hat, kann später wenn er will auch in die Strömungslehre einsteigen und realitätsnäher. über Autos im Regen nachdenken.
An Elektroheizer:
Es war hier nicht von Second-Order-Effekten die Rede, sondern es ging um klar definierte Verhältnisse in einem idealen System. Da die so entstehende Aufgabe recht simpel ist, verstehe ich deinen Einwand nicht.
Alles Gute.
Wie wäre es an der Stelle mal mit der Geometrie der Scheibenwischer. Ist sicher auch ein interessantes Feld.
Oder die Frage: Unter welchen Umständen kann man auf einen Heckscheibenwischer verzichten?
Mir gefällt nicht, dass du dir angewöhnt hast, stur irgendwelche Regeln anzuwenden oder auswendig zu lernen, ohne zu verstehen, was du damit machen kannst.
Deshalb erst mal zur Aufgabe, damit wir uns wenigstens verstehen.
Der Tropfen legt in dieser Zeit T1 genau die projizierte Höhe y der Scheibe als Weg zurück, während das Auto in horizontaler Richtung in derselben Zeit T1 genau die projizierte Tiefe der Scheibe x zurücklegt. Damit hast du nun eine unbekannte Geschwindigkeit von Tropfen und Auto, die im Verhältnis der beiden x- und y- Komponenten der Scheibe als jeweilige Strecke liegen muss.
v (Regen) = y : T1
v (Auto) = x : T1
Also verhalten sich die Geschwindigkeiten im Lösungsfall genau wie die Katheten des Dreiecks, bei dem die Hypotenuse die Lage und Größe der Scheibe ist.
Du kannst das gern mit einem Winkel ausdrücken, den du beliebig eintragen darfst. Ab da aber gilt genau diese deine Skizze als definiert, und du bewegst dich exakt in diesem deinen System nach den dafür zutreffenden Regeln der Trigonometrie.
Lösungsweg 1:
Du hast den Innen-Winkel unten eingetragen als Alpha. Dann ist DEINE Lösung:
tan (Alpha) = Gegenkathete zu Ankathete = vR : vA.
Ich denke, das kannst du selbst nach vA auflösen….
Lösungsweg 2:
Du nutzt in deiner Skizze den oberen Winkel (wir nennen ihn hier Beta).
Die Geometrie ist dieselbe, schließlich ist es dasselbe Auto und dieselbe genau gleich geneigte Heckscheibe (logisch!).
Das einzige, was sich ändert, ist nun die Winkelbeziehung.
tan (Beta) = Gegenkathete zu Ankathete = vA : vR (warum? In deinem jetzt anders definierten rechtwinkligen Dreieck entspricht nun x der Gegenkathete und y der Ankathete)
Auch das kannst du nun nach vA auflösen. Und im rechtwinkligen Dreieck gilt in deinen beiden Skizzen im Vergleich:
Beta + Alpha = 90 Grad
Du siehst, es kommt nicht darauf an, wo du den Winkel einträgst, wenn du damit richtig umgehst…..
Wende das einfach mal an…. Nur mit “selbst rechnen” lernst du etwas.
Viel Erfolg!
schneller als vR /tan (alpha)
Das war nicht die Frage
ja – das war nur die richtige Antwort.
Wer hat danach gefragt? Lies vllt die Fragen zu Ende