I don't understand… Why is it allowed to shorten it like that?
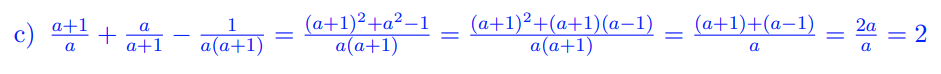
To add two fractions together, they must have the same denominator. That makes sense, but…
In the first step, the square (power of 2) arises because when we add the denominators (the principal part of the fraction) together, we get 2x a(a+1). But why does (a+1)(a-1) suddenly appear in the second step?
And how do you get that this becomes (a+1)+(a-1)/a? And why does 2a/a simply equal 2? After all, we don't even know what a is. Why can we just remove the a? HUH
(However, the problem states that a is a real number and can be neither -1 nor 0.)
I don't understand.
(0 rating, 0 votes, rated)You need to be a registered member to rate this.
Loading...
After the third binary formula
a2-1 = (a+1)*(a-1)
of course. Then the counter a+1 is clipped out
and against the a+1 in the denominator.
Have you ever applied the third binary formula?
and now set b=1 and read the equation from right to left.
2a/a you can cut away. Because there is 2 * a. If there is (2+a) / a, you should not be short.
The second step is because you have to match the denominators of the first three fractures. You have to factor. If you multiply a break, for example, then you must also multiply the counter with a.